車輛行駛在凹凸不平路面上所引起車架上下的移動是一個隨機變量。因此車架的靜強度分析是隨機靜強度分析問題。現在解決這類問題常用的有限元分析方法有，攝動隨機有限元法，隨機模擬法和正交展開法等。盡管上述方法可以比較準確地對隨機結構做強度計算，但是到目前為止隨機有限元的研究和開發工作還遠遠不及普通的有限元算法。因此，有必要研究一種有效的利用現有功能強大的大型有限元法通用程序對隨機結構進行分析計算的方法。這里在此將討論用粗糙集理論求解隨機靜強度分析問題。粗糙集理論是由波蘭數學家Z.Pawlak于1982年提出的理論，現在己成為當今研究的熱點之一，研究領域廣泛涉及信息、計算機、管理、醫學、化學、材料等學科。由于這種理論與概率方法處理不確定性問題的顯著區別在于它無需提供問題所需處理的數據集合之外的任何先驗信息，所以這兩者之間有很強的互補性。
      在各類工程結構中，存在著很多不確定因素。除了上面所述的車輛在路面的凹凸不平引起車架在車輪附近部位向上或下相對位移荷載外，還有車架結構的物理性質、幾何參數以及所承受的其它荷載。由于條件所限使得人們不能事先確定其數值的大小。這類不確定因素通常被處理為隨機變量。隨機變量定義為:設隨機實驗的樣本空間，如果對于每一個、E都有唯一的一個實數X(與之對應，這樣就得到一個定義在樣本空間n上的實單值函數為隨機變量記為X(w)或X}隨機變量X取值不超過任意實數x的概率P(X)稱為X的分布函數記為，對于任意由上述定義可知，當引入置信度概念后，隨機變量可轉換為在所選擇的置信度或風險下，粗糙集上、下近似集意義上的一個具體的數值或一個區間值。對于具有凸、對稱概率密度函數性質的隨機變量來說，對應的是僅包含一個點的下近似集意義下的數值。因此在以下的討論將僅對由上近似集得到的區間數進行。對于一個含有隨機變量的結構即隨機結構，按照這種方法，在取單側置信上、下限時，隨機變量可以轉化為一個具體的數值。這時把該值代入普通有限元法的程序計算，可得到對隨機結構分析結果的上或下限的結果。對于雙側置信區間時，隨機變量將轉化為一個區間數。把區間數值代入普通的有限元方程中，利用區間算法，將得到區間結果。下面將對求解區間數的有限元法方程進行討論。
      這里所討論的是利用現有的有限元程序進行計算，下面提出幾種方法。即把所有的區間數中對結構影響大的量值組成不同的數據組合都用有限元程序進行計算，然后從中找出計算結果的區間值。如果把區間按等間隔劃分后，用不同的排列組合進行抽樣，就是概率統計理論中的機械抽樣法;如果在區間內進寧示隨機抽樣，則是著名的Monte-Car抽樣法。由文獻，當把區間數方程組解法與結構有限元法的力學意義相結合，可以得到較為簡單的計算方法。當作用在結構上的外載是隨機載荷時，不妨先考察在二維平面單元下的分布載荷是隨機載荷的情況。在確定置信度C后，隨機載荷轉變為區間數，當隨機參數的區間數與有限元方程運算結果之間不滿足單調函數的關系時，用有限元計算的結果例如位移與結構參數例如外載荷之間不滿足單調增或單調減的關系。因此若僅把結構隨機參數的區間左、右端點值代入有限元平衡方程之中將不能得到正確的位移區間的結果。因此必須利用力學的基本概念進行判斷，找出除了隨機變量置信區間兩個端點之外的那些能對計算結果產生較大影響的值。然后再從這些結果之中找出位移的區間值。
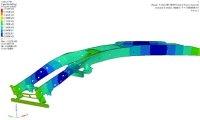
      某小型越野車車架結構如圖所示，車架結構主要由空心圓柱鋼組成，其橫截面內(半)徑為0.025m，外(半)徑0.04m。在底架部位有少數槽型鋼，橫截面高度為0.058m，寬度為0.035m厚度為0.02m。材料的彈性模量為2.1xe11MPa，泊松比0.3。根據汽車車架強度校核方法，首先對汽車在滿載總重量為2000kg且在四輪著地的情況下進行靜強度分析。

                                                                                  專業從事機械產品設計│有限元分析│強度分析│結構優化│技術服務與解決方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.yw15777.cn，轉載請注明出處和相關鏈接！